Come ho imparato ad amare i numeri immaginari

Ho molta difficoltà nel visualizzare cosa sarebbe la Fisica teorica, o la Scienza in generale, senza i numeri immaginari. Non fraintendermi, il mondo esisterebbe lo stesso e la Terra continuerebbe a girare attorno al Sole. Dico solo che senza l’ausilio dei numeri immaginari faremmo molta più fatica nella costruzione di tantissime teorie della Fisica.
Ma il vantaggio non è solo teorico, questi speciali numeri sono così utili che anche gli ingegneri non saprebbero proprio farne a meno, dalla fluidodinamica fino alla teoria dei segnali elettrici.

Cosa c’è di immaginario nei numeri immaginari?

Alla fine ha poco senso definire un numero “immaginario” o reale, in quanto la matematica è di fatto un’invenzione umana e possiamo decidere a piacere cosa sia “reale” o meno.

Invece mi piace pensare che l’aggettivo “immaginario” si riferisca piuttosto a una qualità particolare di chi li ha pensati per la prima volta. Chi ha scoperto questi numeri era una persona ricca di immaginazione, disposta a fare quel passo in più e a sfidare lo status quo. Una persona che ha saputo sfruttare il potere del pensare in grande, del “e se fosse..?“. Alla fine questa è la storia di un “bighellonare produttivo”.

Il bighellonare produttivo

I matematici del XVI secolo erano maggiormente indaffarati con la fondazione dell’algebra e della geometria analitica. Nel frattempo si divertivano a risolvere alcuni “cruciverba“ come: “trova le radici dell’equazione polinomiale x²+3x-4=0 usando gli assiomi dell’algebra”. Era importante specificare “usando gli assiomi dell’algebra” perché, come ogni gioco, anche la matematica ha le sue regole. Ad esempio sarebbe facile, in una partita di calcio, prendere la palla con le mani e lanciarla verso la porta per fare gol, ma a quel punto staremmo parlando proprio di un altro sport. La matematica è tale proprio per via delle sue regole.

Le regole del gioco della matematica di allora prevedevano che fosse proibito affermare che il quadrato di un numero potesse essere un numero negativo: “meno per meno fa più, e più per più fa più“. Se così non fosse, romperemmo ogni logica del gioco. Queste regole impedivano che alcune equazioni polinomiali avessero una soluzione. Ad esempio x²-2x+2=0 non ammette soluzioni: non esiste un numero “x” che inserito in quella equazione dia zero come risultato. Graficamente stiamo parlando di una parabola che non tocca mai l’asse y=0

Un modo semplice di vedere perché l’equazione non ha soluzioni è con un cambio di variabile:

Cioè, definendo t=x-1, risolvere x²-2x+2=0 equivale a risolvere:

È quindi chiaro perché quella parabola non tocca mai lo zero! Se lo facesse staremmo rompendo le regole del gioco: il quadrato di un numero non può mai essere negativo.

Il matematico italiano Gerolamo Cardano sapeva bene che qualcosa come x²-2x+2=0 non ammette soluzioni, eppure decise di bighellonarci attorno. Cardano fece finta che in qualche modo fosse possibile che un numero al quadrato potesse essere negativo. Possiamo immaginare che forse lo fece per gioco, o magari per puro sfizio, in ogni caso si divertì a scrivere la radice quadrata di -1:

Et voilà, ora anche x²+1=0 ammette due soluzioni come moltissime altre equazioni di secondo grado.
Questa soluzione non fu presa sul serio dai matematici dell’epoca. Rafael Bombelli, altro matematico italiano che osò bighellonare su queste questioni, definiva queste soluzioni “quantità silvestri“.

Questo piccolo passo segnò però l’inizio di una nuova comprensione della matematica: si possono modificare le regole del gioco e riuscire comunque a creare dei costrutti logici autoconsistenti.

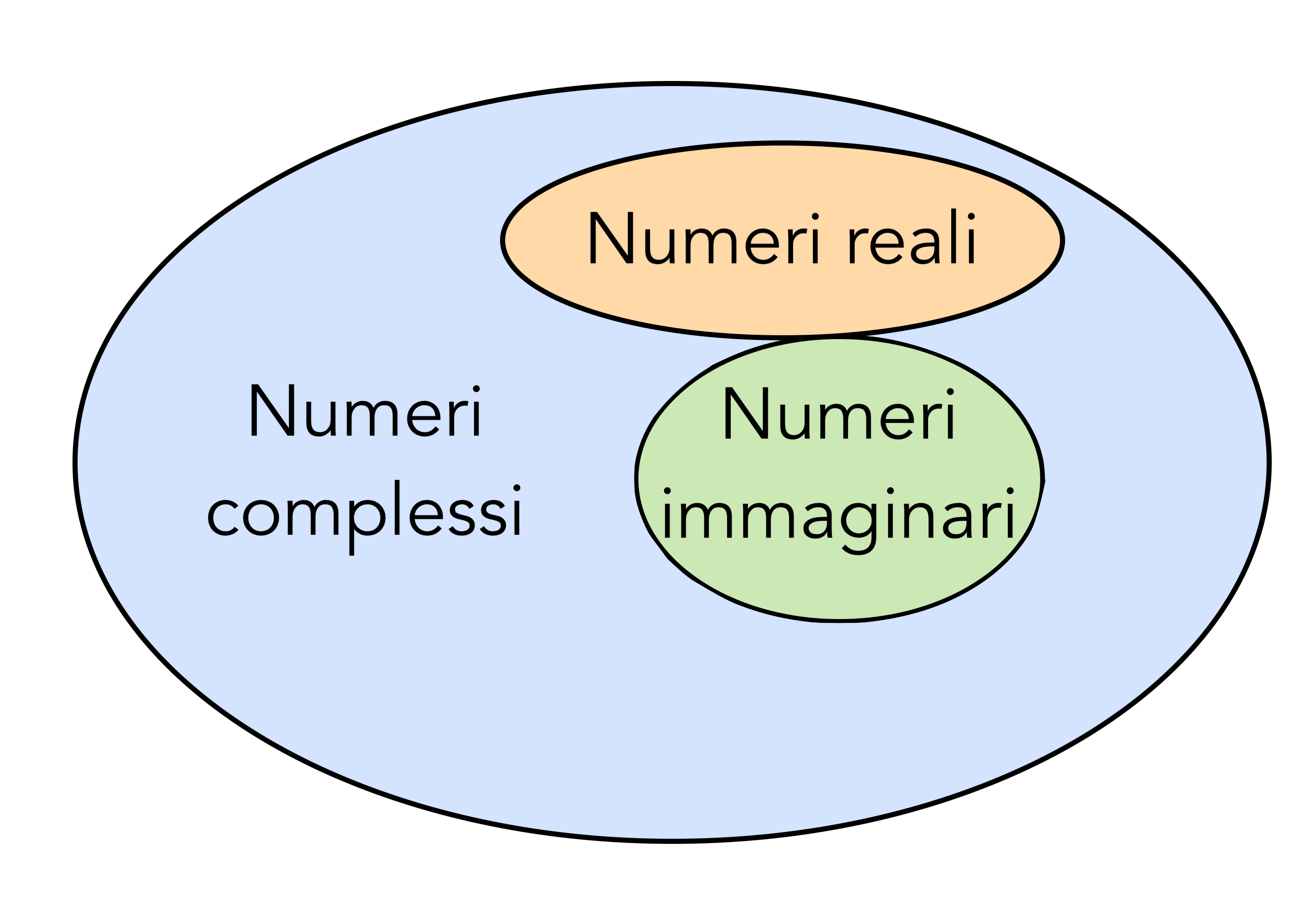
Chiaramente la radice quadrata di un numero negativo non può essere rappresentata sul piano cartesiano, perché è un numero che rompe le regole dei numeri cartesiani di tutti i giorni. Ma per questo motivo non è un numero che ha meno diritti degli altri, è semplicemente un numero diverso che merita il proprio “asse cartesiano”, magari con un nome diverso. I matematici dei secoli successivi definirono quindi i numeri immaginari come un’estensione dei numeri reali, aventi la loro algebra e i loro assiomi.

Torniamo però un attimo alla soluzione di x²-2x+2=0. Avevamo visto che questa era equivalente a risolvere t²=-1 che ha due soluzioni immaginarie date dalla radice di -1. Avevamo definito t=x-1, quindi possiamo scrivere la soluzione con la variabile originale

Quindi la soluzione non è un numero puramente immaginario: il numero “1″ è un numero “normalissimo”, reale, che rispetta gli assiomi dei numeri reali. Tuttavia è sommato (o sottratto) con un numero immaginario (la radice di -1). Che senso ha, e come può essere rappresentato questo numero? I matematici lo definirono numero complesso, cioè un ibrido tra numero reale e numero immaginario.

Un numero complesso venne definito come un oggetto costituito da due parti: una parte reale e una parte immaginaria. La parte reale e la parte immaginaria sono rappresentate comunque da numeri reali, quindi in un certo senso un numero complesso non è altro che una coppia di numeri reali che soddisfa alcune proprietà speciali. Vedremo tra poco il senso di questa affermazione.
Per comodità di notazione fu definito un simbolo speciale per l’unità immaginaria, “i“, in modo che ogni numero immaginario sia un suo multiplo:

Un numero complesso “z” può essere espresso con più notazioni equivalenti:

La cosa curiosa è che la notazione con le parentesi (parte reale, parte immaginaria) ricorda quella utilizzata per rappresentare i vettori in due dimensioni (componente x, componente y). Questa cosa è del tutto intenzionale, come vedremo tra poco.

Dal XVIII secolo in poi i numeri complessi vennero considerati un’estensione dei numeri reali, nel senso che un numero reale non è altro che un numero complesso con parte immaginaria nulla.

Con molta astuzia, furono identificate delle operazioni di somma e prodotto di numeri complessi che rendessero tutto autoconsistente.

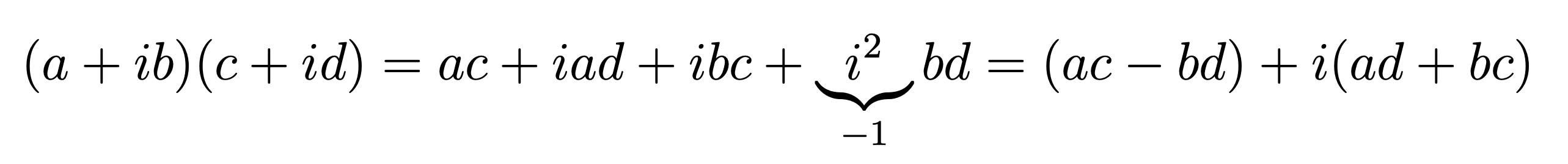
Cosa mi ha fatto amare i numeri immaginari

I matematici capirono presto che per i numeri complessi esisteva un’interpretazione geometrica piuttosto semplice, ed è per questo motivo che scelsero di rappresentarli con una notazione simile a quella usata per i vettori in due dimensioni.

La volta che mi affezionai ai numeri immaginari fu quando realizzai quanto fossero utili in un contesto geometrico. A un certo punto mi si sbloccò il seguente ragionamento.
Prendiamo un vettore a componenti reali, innocentissimo, bidimensionale: una freccia. Se moltiplichiamo il vettore per il numero “-1” ne invertiamo la direzione:

Siccome i vettori possono essere ruotati sul piano, possiamo interpretare l’inversione come una rotazione di un angolo piatto!

Quindi il numero -1 è un numero molto speciale perché esegue la stessa mansione di una rotazione di 180 gradi.

Il punto è che potremmo anche arbitrariamente pensare che la rotazione di 180 gradi sia un processo a due step, una composizione di due rotazioni di 90 gradi:

Uno può quindi chiedersi: esiste un numero speciale in grado di ruotare un vettore di 90 gradi moltiplicando entrambe le sue componenti per esso?
Assumiamo che esista, a quel punto dobbiamo riconoscere che moltiplicare il vettore due volte consecutive per questo numero equivale a ruotare il vettore di 180 gradi, e quindi questo numero deve avere a che fare con “-1″, perché esegue la stessa azione

Quindi se il vettore è ruotato di 180 gradi deve valere

Quindi il quadrato di questo numero deve dare -1: deduciamo che “a=i”, cioè proprio l’unità immaginaria.

Questa è stata la connessione che mi ha fatto apprezzare i numeri complessi: possono essere utilizzati per ruotare degli oggetti! Per questo motivo i matematici inventarono un piano cartesiano dedicato ai numeri complessi, il piano di Gauss!

In questo piano abbiamo due assi: l’asse reale e l’asse immaginario. Un numero complesso è “molto simile” a un vettore, perché ha una componente reale a una componente immaginaria date dalle proiezioni su questi assi ortogonali:

Il vantaggio algebrico di avere un numero che moltiplicato per se stesso dà “-1” è il potere di ruotare degli oggetti moltiplicandoli tra loro!

Se prendiamo come riferimento l’angolo tra il numero complesso e l’asse reale, la moltiplicazione di due numeri complessi ha l’effetto di produrre un nuovo numero complesso avente come nuovo angolo la somma degli angoli iniziali, come mostrato in figura:

Infatti si ha, per le regole stabilite sopra:

E questa è secondo me la principale utilità dei numeri complessi: ci permettono di trasformare oggetti usando la notazione più compatta possibile.

Infatti se “ρ” è il modulo del numero complesso (definito proprio come il modulo dei vettori):

Allora possiamo scrivere le componenti reale e immaginaria usando la trigonometria proprio come si fa per i vettori in notazione polare. Se θ è l’angolo formato con l’asse reale si ha

La quantità tra parentesi (che ha modulo unitario per via della relazione trigonometrica fondamentale) può essere semplificata usando una relazione utilissima dimostrabile in analisi matematica, la quale lega il numero di Eulero con i numeri complessi:

Quindi un numero complesso può essere espresso con la elegantissima notazione

La moltiplicazione di due numeri complessi ha quindi il seguente effetto:

Con questa notazione è anche più facile vedere che gli angoli si sommano, grazie alla proprietà degli esponenziali.

In sostanza, i numeri complessi sono davvero uno spasso (di sicuro sono meno monotoni dei numeri reali), ma prima di tutto sono i numeri più popolari della Scienza:

• Moltissime trasformazioni nella fisica teorica sono generate da operatori complessi. Alcune tra le più importanti equazioni del Modello Standard sono scritte in notazione complessa.
• In ingegneria, la teoria dei segnali è fondata sull’utilizzo dei numeri complessi.
• In aerodinamica, l’analisi complessa è utilizzata per mappare il flusso dei fluidi attorno ad alcuni oggetti.
• ….
  

Di sicuro potremmo fare tutte queste cose anche senza i numeri complessi, solo che faremmo molta più fatica! I numeri complessi sono una short-cut, ci semplificano la vita ogni giorno, e per questo dovremmo amarli.

Tuttavia a volte non si tratta solo di semplificare la vita. Di recente ho incrociato un articolo su Physics Today che parlava della necessità dei numeri complessi nella meccanica quantistica.
In sostanza, non solo non esiste un modo semplice per formulare la meccanica quantistica usando solo variabili reali, ma la versione della teoria senza numeri complessi non è in grado di replicare le previsioni sperimentali della teoria complessa. Questa conclusione mi ha lasciato un po’ sorpreso, dato che implicherebbe una supremazia quasi metafisica dei numeri complessi. Ho quindi intenzione di approfondirla in un prossimo articolo, dopo che mi sarò informato adeguatamente.

• Esercizio: come ultima chicca ti sfido a scoprire una cosa che ritengo molto carina. Prendi la relazione di Eulero:

Questa è un’identità, quindi l’uguaglianza vale per qualsiasi valore di θ. Ti invito a inserirci θ=π/2 e usare quanto sai sul valore di seno e coseno per l’angolo retto. Dopodiché eleva entrambi i membri per “i”, cosa ottieni?

---

PS. ho scritto un libro di testo che rappresenta proprio ciò che avrei desiderato leggere all’inizio dei miei studi di Fisica teorica, per renderla accessibile agli amatori e insegnare le tecniche matematiche necessarie a una sua comprensione universitaria. Si chiama “L’apprendista teorico” , dai un’occhiata per vedere di cosa si tratta. Il libro è acquistabile su Amazon.