Per capire l’entità del contributo di Enrico Fermi in ciò che servì ad ispirare una delle scoperte più importanti dell’umanità (la teoria dei semiconduttori), è necessario fare qualche passo indietro e considerare il contesto storico-scientifico dell’epoca.
Negli anni ’20 del secolo scorso si sapeva molto poco sulle strutture fondamentali della materia. Le teorie dell’atomo erano giovanissime e l’unico metodo di indagine consisteva nell’osservare l’assorbimento luminoso di alcuni gas della tavola periodica.

Proprio sui gas si sapeva dire un po’ di più, essendo una collezione di atomi che potevano essere trattati (in certe condizioni di densità e temperatura) come un grosso insieme di biglie microscopiche su cui, tramite la fisica statistica di Maxwell, Boltzmann e Gibbs, si potevano fare previsioni termodinamiche verificabili sperimentalmente.
Una particolarità interessante della teoria statistica di Maxwell e Boltzmann era il contenuto minimale di ipotesi sulla natura fisica di queste “biglie microscopiche”. Stiamo parlando di una teoria formulata nella seconda metà del secolo XIX, un periodo in cui non era ancora riconosciuta l’esistenza dell’atomo!
Trattandosi tuttavia di atomi, nemmeno la teoria di Maxwell e Boltzmann uscì indenne dalla rivoluzione della teoria dei quanti, iniziata con Planck nel 1900.
La teoria dei quanti funzionò sia da completamento che da antidoto per la vecchia fisica statistica. Da antidoto perché aiutò ad indagare meglio alcuni problemi matematici della teoria di Maxwell e Boltzmann, i quali conducevano a calcoli errati nella trattazione di particelle tra loro indistinguibili, e davano dei risultati impossibili per alcune quantità come l’entropia dei gas a basse temperature.
Un problema statistico dell’entropia
Queste difficoltà erano dovute al fatto che la fisica statistica si basa essenzialmente sul “contare, per tutte le particelle, tutte le possibili configurazioni microscopiche che conducono alla stessa situazione fisica del gas“, come illustrato in figura:

Pressione, volume, temperatura ![]() , sono tutte quantità macroscopiche misurabili sperimentalmente. In fisica statistica ci immaginiamo di conoscere le posizioni e velocità di tutte le particelle del gas in ciascuna configurazione possibile ammessa dalle condizioni ambientali (cosa non possibile da un punto di vista computazionale, ma che facciamo finta di poter fare comunque).
, sono tutte quantità macroscopiche misurabili sperimentalmente. In fisica statistica ci immaginiamo di conoscere le posizioni e velocità di tutte le particelle del gas in ciascuna configurazione possibile ammessa dalle condizioni ambientali (cosa non possibile da un punto di vista computazionale, ma che facciamo finta di poter fare comunque).
Siccome non sappiamo in quale configurazione microscopica precisa si trovi il gas in ciascun istante di tempo (non è misurabile sperimentalmente), immaginiamo di avere ![]() copie del nostro gas e di fare delle estrazioni per contare quante volte esce una certa configurazione piuttosto che un’altra. La distribuzione di queste estrazioni definisce alcune quantità macroscopiche
copie del nostro gas e di fare delle estrazioni per contare quante volte esce una certa configurazione piuttosto che un’altra. La distribuzione di queste estrazioni definisce alcune quantità macroscopiche ![]() associate alla specifica configurazione microscopica
associate alla specifica configurazione microscopica ![]() estratta un numero
estratta un numero ![]() di volte. Le quantità macroscopiche
di volte. Le quantità macroscopiche ![]() che misuriamo sperimentalmente possono quindi essere pensate come la media di tutte le
che misuriamo sperimentalmente possono quindi essere pensate come la media di tutte le ![]() pesate con la probabilità di estrazione
pesate con la probabilità di estrazione ![]() .
.
La misura sperimentale di
ci dà quindi informazioni sulla distribuzione delle configurazioni microscopiche del nostro gas.
Immaginando il gas in equilibrio termico a una certa energia interna, il numero di configurazioni del gas corrispondenti a tale energia possono essere contate, dal punto di vista teorico, sommando tutte le possibili accoppiate di posizione-velocità ![]() nelle tre dimensioni spaziali, e ciò deve essere fatto per tutte le particelle del gas.
nelle tre dimensioni spaziali, e ciò deve essere fatto per tutte le particelle del gas.
Siccome il numero di possibili accoppiate è virtualmente infinito, i padri fondatori della fisica statistica immaginarono di dividere lo spazio dei possibili valori di posizione e velocità in cellette elementari di dimensione finita che chiamiamo ![]() . In questo modo due stati dinamici specificati da
. In questo modo due stati dinamici specificati da ![]() ,
,![]() e
e ![]() ,
,![]() che caschino nella stessa celletta di questo spazio sono considerati essere lo stesso stato dinamico. È come se ammettessimo, in un certo senso, di non sapere distinguere tra
che caschino nella stessa celletta di questo spazio sono considerati essere lo stesso stato dinamico. È come se ammettessimo, in un certo senso, di non sapere distinguere tra ![]() ,
,![]() e
e ![]() ,
,![]() nel caso appartengano alla stessa cella, è un’approssimazione.
nel caso appartengano alla stessa cella, è un’approssimazione.

Dal punto di vista statistico, l’entropia del gas è pensabile come una misura di quanti stati dinamici microscopici sono associabili a un certo stato termodinamico macroscopico, una misura della nostra “ignoranza” sull’effettiva configurazione microscopica del gas.
Il problema era che la dimensione ![]() della celletta elementare era del tutto arbitraria, e ciò influiva pesantemente sul conteggio delle configurazioni. Essendo il numero delle configurazioni direttamente collegato alla definizione statistica di entropia, una scelta di
della celletta elementare era del tutto arbitraria, e ciò influiva pesantemente sul conteggio delle configurazioni. Essendo il numero delle configurazioni direttamente collegato alla definizione statistica di entropia, una scelta di ![]() troppo piccola conduceva a valori infiniti per l’entropia del gas. Questa indeterminazione sulla scelta di
troppo piccola conduceva a valori infiniti per l’entropia del gas. Questa indeterminazione sulla scelta di ![]() impediva inoltre di calcolare, statisticamente, il valore della costante dell’entropia alla temperatura dello zero assoluto.
impediva inoltre di calcolare, statisticamente, il valore della costante dell’entropia alla temperatura dello zero assoluto.
Il problema della costante dell’entropia stava molto a cuore ai fisici dell’epoca. Nella termodinamica ottocentesca ci si interessava solo alle differenze di entropia, e quindi era di scarso interesse pratico domandarsi quale fosse il valore assoluto dell’entropia a una determinata temperatura come ![]() , e in ogni caso questa costante spariva quando si faceva la differenza
, e in ogni caso questa costante spariva quando si faceva la differenza ![]() tra due stati termodinamici
tra due stati termodinamici ![]() e
e ![]() .
.
Tuttavia con l’arrivo del teorema di Nernst e quindi del terzo principio della termodinamica (il quale postula che l’entropia allo zero assoluto sia esattamente zero) si rivelò essenziale determinare il valore di questa costante.
Un altro problema fastidioso era quello che riguardava il conteggio di particelle indistinguibili: quando si contavano tutte le configurazioni possibili di tutte le particelle del gas si finiva per contare più volte la stessa configurazione per via del fatto che non è possibile distinguere una particella dall’altra. Per via di ciò si arrivava a dei paradossi che riguardavano l’entropia di mescolamento dei gas.
Di questo problema si interessò Gibbs, il quale propose di dividere i conteggi per il fattore combinatorico ![]() dove
dove ![]() è il numero di particelle e con “!” si intende il fattoriale
è il numero di particelle e con “!” si intende il fattoriale ![]() .
.
Tuttavia anche questa soluzione non risolveva tutti i problemi…
La teoria dei quanti sistemò i problemi dell’entropia. Si dimostrò che la dimensione ![]() delle cellette elementari doveva essere pari alla costante di Planck
delle cellette elementari doveva essere pari alla costante di Planck ![]() : la natura discreta della teoria quantistica si sposava bene con l’ipotesi delle cellette elementari della fisica statistica.
: la natura discreta della teoria quantistica si sposava bene con l’ipotesi delle cellette elementari della fisica statistica.
Il punto è che gli effetti quantistici delle particelle non sono più trascurabili a basse temperature. In fisica statistica esiste una quantità chiamata lunghezza d’onda termica di De Broglie, la quale ha la seguente espressione per un gas perfetto monoatomico:

 è la costante di Planck,
è la costante di Planck,  la massa delle particelle,
la massa delle particelle,  la costante di Boltzmann che converte da dimensioni di energia a dimensioni di temperatura tramite
la costante di Boltzmann che converte da dimensioni di energia a dimensioni di temperatura tramite 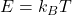 , e
, e  la temperatura del gas.
la temperatura del gas.Questa lunghezza d’onda deriva dalla formulazione ondulatoria di De Broglie per le particelle quantistiche.
Secondo De Broglie, a ogni particella avente quantità di moto ![]() è associabile una lunghezza d’onda
è associabile una lunghezza d’onda ![]() . Se come
. Se come ![]() si prende la quantità di moto termica delle particelle del gas si ottiene la
si prende la quantità di moto termica delle particelle del gas si ottiene la ![]() riportata sopra.
riportata sopra.
A temperature normali questa lunghezza d’onda è molto più piccola della distanza media tra gli atomi di un gas. Vediamo però che al diminuire di ![]() , la relazione di inversa proporzionalità
, la relazione di inversa proporzionalità ![]() aiuta a far crescere questa lunghezza d’onda. Per temperature sufficientemente basse la lunghezza d’onda
aiuta a far crescere questa lunghezza d’onda. Per temperature sufficientemente basse la lunghezza d’onda ![]() diventa comparabile con le distanze inter-atomiche del gas.
diventa comparabile con le distanze inter-atomiche del gas.

Nel caso in figura sono mostrati dei bosoni.
Quindi, per via delle loro proprietà quantistiche, le particelle iniziano ad interferire tra loro come tante onde, e questo succede quando la loro lunghezza d’onda diventa almeno comparabile con la distanza tra una particella e l’altra, a temperature molto basse.
Siccome parliamo di funzioni d’onda che creano interferenze, l’indistinguibilità delle particelle gioca un ruolo centrale in questo processo quantistico, e ciò sta alla base di tutte le difficoltà teoriche della vecchia fisica statistica, la quale non teneva conto di queste proprietà quantistiche. Fino alla prima metà degli anni ’20, questa sottigliezza quantistica non era ancora stata compresa in profondità.
Statistica quantistica: la strada di Fermi

Ancora fresco di laurea, Fermi divenne particolarmente ossessionato dal problema della costante dell’entropia, pubblicando diversi articoli tra il 1924 e il 1926.
Aveva intuito che il problema risiedesse nella natura quantistica delle particelle, in particolare dal punto di vista della loro indistinguibilità, ma mancava ancora qualche pezzo del puzzle.
Il pezzo mancante fu messo a disposizione da Pauli con la formulazione del principio di esclusione: non possiamo avere due elettroni con tutti i numeri quantici uguali tra loro. Gli elettroni sono particelle indistinguibili, quindi Fermi si ispirò al loro comportamento per provare a quantizzare un gas di particelle a temperature sufficientemente basse.
Possiamo immaginarci un Fermi che lavora assiduamente all’alba (il suo momento preferito per studiare e lavorare su nuovi articoli) in qualche fredda mattina di Firenze, nell’inverno del 1925-26, sforzandosi di sfruttare il principio di Pauli per ottenere la costante corretta dell’entropia allo zero assoluto.

Nel suo articolo “Sulla quantizzazione del gas perfetto monoatomico” uscito nel febbraio del 1926, Fermi ipotizzò che un gas ideale si comportasse proprio come gli elettroni del principio di Pauli e cambiò completamente il modo di contare le configurazioni possibili in fisica statistica: in ciascuno stato dinamico possono esserci zero o al massimo una sola particella, mai due nello stesso stato.
Immaginò poi che il gas potesse essere caratterizzato da determinati livelli energetici discreti, proprio come si faceva nella quantizzazione dell’atomo di idrogeno. Questa spaziatura tra i livelli energetici era tanto più rilevante per la fisica del problema quanto più era bassa la temperatura del gas, essenzialmente per il motivo enunciato sopra. Ad alte temperature gli effetti quantistici devono essere trascurabili e si ritorna alla termodinamica dell’ottocento.
La conseguenza di questo nuovo modo di contare era che ciascuno stato ![]() era occupato da un numero medio di particelle in funzione dell’energia
era occupato da un numero medio di particelle in funzione dell’energia ![]() dello stato, secondo la seguente espressione:
dello stato, secondo la seguente espressione:

 (o Eulero), l’energia
(o Eulero), l’energia  dello stato, la temperatura
dello stato, la temperatura  , la costante di Boltzmann
, la costante di Boltzmann  . Il parametro
. Il parametro 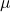 è noto come “potenziale chimico” e allo zero assoluto corrisponde all’energia di Fermi:
è noto come “potenziale chimico” e allo zero assoluto corrisponde all’energia di Fermi: 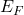 .
.Usando questa informazione, Fermi calcolò l’espressione della costante dell’entropia, la quale coincideva con il valore sperimentale dedotto da Sackur e Tetrode nel 1912. La sua teoria era un successo!
Tuttavia, come confermato anche da alcuni studiosi (Belloni, Perez et al), Fermi non si interessò delle radici quantistiche di questa nuova statistica, cioè non provò a collegare il principio di Pauli con la natura ondulatoria della materia. Inoltre non esisteva, al tempo, un gas capace di comportarsi come gli elettroni dell’articolo di Fermi. La soluzione di Fermi voleva andare nella direzione della statistica quantistica, ma con un approccio molto cauto sulle ipotesi alla base. Fermi utilizzò la sua intuizione per dare una nuova soluzione a dei problemi annosi di fisica statistica (già risolti recentemente da Bose e Einstein con la loro statistica) e dedusse una statistica completamente nuova.
Tuttavia, al contrario di quanto si dice solitamente in giro, Fermi non applicò direttamente questa nuova statistica al problema degli elettroni nei metalli (cosa che fu fatta da altri e che condusse alla teoria dei semiconduttori).
La statistica di Fermi-Dirac
La distribuzione trovata da Fermi è dipendente dalla temperatura. Abbiamo già anticipato che gli effetti quantistici diventano preponderanti a temperature vicine allo zero assoluto. In questo caso il principio di Pauli emerge direttamente dalla forma analitica della distribuzione, riportata in figura:

Man mano che la temperatura del gas di elettroni si avvicina a ![]() , la distribuzione di Fermi si avvicina sempre di più alla “funzione gradino”
, la distribuzione di Fermi si avvicina sempre di più alla “funzione gradino”

Allo zero assoluto, gli elettroni occupano i livelli energetici riempiendoli dal più basso fino a un’energia chiamata “energia di Fermi”, indicata con ![]() .
.
Puoi notare come a ![]() il numero medio di occupazione dello stato a energia
il numero medio di occupazione dello stato a energia ![]() sia esattamente
sia esattamente ![]() : non può esserci più di un elettrone per stato, è il principio di esclusione di Pauli in tutta la sua gloria. Nota anche che non ci sono elettroni che occupano stati a energia maggiore di quella di Fermi.
: non può esserci più di un elettrone per stato, è il principio di esclusione di Pauli in tutta la sua gloria. Nota anche che non ci sono elettroni che occupano stati a energia maggiore di quella di Fermi.

Questo comportamento è essenzialmente verificato anche per temperature più alte di ![]() , basta solo che sia
, basta solo che sia ![]() dove
dove ![]() è detta “temperatura di Fermi”, ed è pari a
è detta “temperatura di Fermi”, ed è pari a ![]() . Nelle situazioni di interesse fisico (come nei metalli), la condizione
. Nelle situazioni di interesse fisico (come nei metalli), la condizione ![]() è praticamente sempre soddisfatta, essendo
è praticamente sempre soddisfatta, essendo ![]() di solito dell’ordine di alcune centinaia di migliaia di gradi kelvin.
di solito dell’ordine di alcune centinaia di migliaia di gradi kelvin.
I gas di elettroni sono fortemente influenzati dal principio di Pauli: è un po’ come se ci fosse una forza “repulsiva” tra gli elettroni, la quale gli impedisce di occupare lo stesso stato energetico. Questa è anche un’interpretazione euristica del fatto che la pressione di un gas di Fermi sia più elevata di un gas classico: è difficile comprimere un gas di elettroni perché non vogliono mai “occupare lo stesso punto spaziale”.
Come mai questa statistica è chiamata “Fermi-Dirac” e non solo “Fermi”?
È noto che Dirac pubblicò la stessa formula alla fine dell’estate del 1926, mentre Fermi l’aveva presentata nella primavera dello stesso anno. Dirac, su sollecito scritto da parte del fisico italiano, ammise di aver letto il lavoro di Fermi, ma sostenne di averlo completamente scordato.
In difesa di Dirac va detto che il suo lavoro (“On the Theory of Quantum Mechanics“) è molto più generale di quello presentato da Fermi, il quale si era invece proposto di risolvere un problema particolare (quello dell’entropia) che c’entrava poco con i postulati della meccanica quantistica.
Dirac giustificò in maniera elegante il principio di esclusione di Pauli notando che la meccanica quantistica era il luogo naturale per trattare i sistemi di particelle indistinguibili, grazie al formalismo delle funzioni d’onda.
La chiave del ragionamento di Dirac si trova proprio nel fatto che le particelle elementari possono essere considerate indistinguibili. La conseguenza quanto-meccanicistica è che se consideriamo due particelle non interagenti tra loro, e che possono occupare gli stati ![]() e
e ![]() , la funzione d’onda che le descrive collettivamente è data dal prodotto delle due funzioni d’onda
, la funzione d’onda che le descrive collettivamente è data dal prodotto delle due funzioni d’onda
![]()
in cui ![]() e
e ![]() sono le posizioni delle due particelle. Se scambiamo le due particelle, e cioè le portiamo dallo stato
sono le posizioni delle due particelle. Se scambiamo le due particelle, e cioè le portiamo dallo stato ![]() allo stato
allo stato ![]() e viceversa, otteniamo la funzione d’onda modificata
e viceversa, otteniamo la funzione d’onda modificata
![]()
Ma se assumiamo che le particelle siano indistinguibili, la densità di probabilità deve restare la stessa (ricordiamo che è data dal modulo al quadrato della funzione d’onda):
![]()
Quindi al massimo possiamo avere che ![]() è diversa da
è diversa da ![]() per un fattore
per un fattore ![]()
![]()
in cui ![]() è un numero tale che
è un numero tale che ![]() in modo da soddisfare
in modo da soddisfare ![]() (verifica pure!).
(verifica pure!).
Se ri-scambiamo le due particelle, torniamo punto e a capo, e cioè deve essere ![]()
![]()
ovvero ![]() , la quale ha soluzione
, la quale ha soluzione ![]() .
.
Se ![]() stiamo parlando di particelle con funzioni d’onda antisimmetriche (cioè lo scambio delle particelle produce un segno meno moltiplicativo nella funzione d’onda totale). Una conseguenza è che se parliamo dello stesso stato
stiamo parlando di particelle con funzioni d’onda antisimmetriche (cioè lo scambio delle particelle produce un segno meno moltiplicativo nella funzione d’onda totale). Una conseguenza è che se parliamo dello stesso stato ![]() allora lo scambio delle particelle produce la seguente relazione
allora lo scambio delle particelle produce la seguente relazione
![]()
la quale implica identicamente ![]() , cioè non esiste uno stato quantistico in cui queste particelle hanno gli stessi numeri quantici. Questa è la giustificazione quanto-meccanicistica del principio di Pauli, e condusse Dirac a ricavare la stessa formula di Fermi per la statistica degli elettroni.
, cioè non esiste uno stato quantistico in cui queste particelle hanno gli stessi numeri quantici. Questa è la giustificazione quanto-meccanicistica del principio di Pauli, e condusse Dirac a ricavare la stessa formula di Fermi per la statistica degli elettroni.

Fermi si limitò all’applicazione del principio di esclusione su un problema specifico, senza provare a darne un’interpretazione quanto-meccanicistica.
In ogni caso, Dirac riconobbe comunque l’importanza del lavoro di Fermi, e propose di chiamare la nuova statistica “Fermi-Dirac”, mettendo il nome di Fermi al primo posto.
Oggi le particelle (come gli elettroni) che obbediscono alla statistica di Fermi-Dirac sono note come “fermioni”, sempre in onore di Fermi. I fermioni sono tutte quelle particelle caratterizzate da uno spin semi-intero. Per un teorema rigorosamente dimostrabile in teoria quantistica dei campi, tutte le particelle a spin semi-intero obbediscono alla statistica di Fermi-Dirac, mentre quelle a spin intero (note come “bosoni“) obbediscono alla statistica di Bose-Einstein (sono le particelle con ![]() dopo uno scambio).
dopo uno scambio).

Alle alte temperature (dove gli effetti quantistici sono meno preponderanti) sia fermioni che bosoni tornano ad obbedire alla statistica di Maxwell-Boltzmann e Gibbs.
PS. ho scritto un libro di testo che rappresenta proprio ciò che avrei desiderato leggere all’inizio dei miei studi di Fisica teorica, per renderla accessibile agli amatori e insegnare le tecniche matematiche necessarie a una sua comprensione universitaria. Si chiama “L’apprendista teorico” , dai un’occhiata per vedere di cosa si tratta. Il libro è acquistabile su Amazon.





chiarissimo come sempre, Matteo