Scoperte verso la fine del 1915, le equazioni di campo di Einstein della Relatività Generale rappresentano uno dei risultati intellettuali più importanti della nostra civiltà.

Queste equazioni descrivono la Gravità in maniera completamente differente dalla legge di gravitazione newtoniana.
La Gravità di Newton è quel fenomeno a cui attribuiamo il moto, nello spazio e nel tempo, degli oggetti che si trovano nei pressi di altri oggetti massivi.
Per Einstein, la Gravità non è un fenomeno di per sé. Lo spazio e il tempo diventano quantità dinamiche, modificabili dalla materia che li riempie. A sua volta, la materia non può fare altro che muoversi nello spazio e nel tempo, con un moto dettato precisamente dalla geometria dello spazio e del tempo.
Parliamoci chiaro: lo spazio-tempo non è un fluido che interagisce con la materia, non è un qualcosa di tangibile, è ancora più pazzesco di così.
Lo spazio-tempo è una collezione di eventi a cui ogni corpo è fondamentalmente legato, perché è con gli eventi che capiamo la realtà. È il nostro modo di comprendere il mondo: “quell’oggetto stava lì, a quell’ora del giorno”.
Dal punto di vista matematico interpretiamo la collezione di eventi come una iper-superficie geometrica in quattro dimensioni (3 spaziali e 1 temporale). È questa la grande intuizione di Einstein.
Le equazioni di Einstein dicono come questa iper-superficie reagisce alla presenza di massa ed energia. Il concetto è semplice, ma le equazioni sono abbastanza complicate.
È quindi mia intenzione decodificarle per dimostrare come funzionano anche ai non-esperti del settore.
Chi è già esperto può invece comodamente leggersi la bibbia della gravitazione di Kip Thorne, J.A. Wheeler e C. Misner.
Per iniziare la decodificazione, concentriamoci sul cosa e sul come: cosa stiamo cercando di risolvere con queste equazioni? E come lo stiamo cercando?
Decodificazione: cosa stiamo cercando?
Siccome è difficile disegnare le iper-superfici a 4 dimensioni, concentriamoci su 3 dimensioni per fissare le idee. Considera questa figura:

Matematicamente, come fai a descrivere questo spazio? Immagina che questo fosse, in origine, un lenzuolo. Un lenzuolo disteso in uno spazio tridimensionale. Il lenzuolo, di per sé, ha due dimensioni (lunghezza e larghezza, se trascuri lo spessore), ma vive in uno spazio tridimensionale in cui possiamo giudicare se il lenzuolo è curvo verso l’alto o verso il basso, proprio come nella figura.
Prendi un pennarello e disegna due punti A e B su questo lenzuolo, come nella figura seguente:

Prendi un sistema di assi cartesiani ![]() e
e ![]() , come si fa a scuola: qual è la distanza più preve tra
, come si fa a scuola: qual è la distanza più preve tra ![]() e
e ![]() ? Naturalmente è data dal teorema di Pitagora
? Naturalmente è data dal teorema di Pitagora
![]()
dove ![]() e
e ![]() . Questa è chiamata geometria piatta di uno spazio, è tutto liscio, nessun rigonfiamento, nessuna depressione. Nelle coordinate
. Questa è chiamata geometria piatta di uno spazio, è tutto liscio, nessun rigonfiamento, nessuna depressione. Nelle coordinate ![]() e
e ![]() vale sempre:
vale sempre:
![]()
Questa quantità si chiama metrica (![]() significa
significa ![]() per
per ![]() molto vicino ad
molto vicino ad ![]() , cioè distanze molto piccole). I coefficienti davanti agli elementi
, cioè distanze molto piccole). I coefficienti davanti agli elementi ![]() e
e ![]() (che sono pari a
(che sono pari a ![]() come vedi) si chiamano coefficienti della metrica, che è indicata come un oggetto a quattro componenti:
come vedi) si chiamano coefficienti della metrica, che è indicata come un oggetto a quattro componenti: ![]() . Siccome non ci sono termini misti del tipo
. Siccome non ci sono termini misti del tipo ![]() diremo che questi hanno coefficiente zero davanti a loro. La metrica è un modo molto comodo di riassumere i contenuti geometrici di uno spazio.
diremo che questi hanno coefficiente zero davanti a loro. La metrica è un modo molto comodo di riassumere i contenuti geometrici di uno spazio.

In questo caso abbiamo ![]() ,
, ![]() ,
, ![]() .
.
Se adesso pieghi il lenzuolo (ti è concesso stiracchiarlo sfruttandone l’elasticità), vedrai i punti precedentemente disegnati cambiare la loro posizione relativa. In uno spazio curvo la metrica ha un’espressione ben diversa da questa che abbiamo appena scritto.

Potremmo essere interessati a capire come varia questa metrica da punto a punto: quanto rapidamente si inclina verso l’alto? Quanto si inabissa? Potremmo chiederci: quanto varia ![]() in vista di un leggero spostamento nella direzione
in vista di un leggero spostamento nella direzione ![]() ? Il cambiamento della metrica lo indichiamo con
? Il cambiamento della metrica lo indichiamo con ![]() .
.

Il simbolo ![]() significa un cambiamento
significa un cambiamento ![]() molto piccolo, nella direzione di
molto piccolo, nella direzione di ![]() , tenendo la coordinata
, tenendo la coordinata ![]() inalterata. Un modo ancora più conciso di scrivere
inalterata. Un modo ancora più conciso di scrivere ![]() è con il simbolo
è con il simbolo ![]() .
.
Un piccolo check: se la metrica è piatta posso spostarmi nella direzione ![]() o
o ![]() quanto voglio, ma lei non cambierà, non si innalza e non si inabissa, quindi
quanto voglio, ma lei non cambierà, non si innalza e non si inabissa, quindi ![]() e
e ![]() .
.
Questo è il punto più importante che serve per capire le equazioni di Einstein.
Esiste una quantità chiamata “curvatura dello spaziotempo” la quale è una combinazione non lineare di termini come ![]() ,
, ![]() ,
, ![]() per le tre dimensioni spaziali, e
per le tre dimensioni spaziali, e ![]() per la dimensione temporale indicata col simbolo
per la dimensione temporale indicata col simbolo ![]() . Le informazioni sulla curvatura sono racchiuse in simboli che indichiamo con
. Le informazioni sulla curvatura sono racchiuse in simboli che indichiamo con ![]() e
e ![]() :
:

 sta a significare “come varia la variazione della metrica”? Allo stesso modo in cui l’accelerazione ci dice come varia la variazione della posizione (cioè come varia la velocità).
sta a significare “come varia la variazione della metrica”? Allo stesso modo in cui l’accelerazione ci dice come varia la variazione della posizione (cioè come varia la velocità).Einstein voleva un’equazione che esprimesse la seguente frase: “questa distribuzione di massa ed energia fa sì che la metrica varii da punto a punto (tramite ![]() ) in questo modo qui. Sai trovare la metrica
) in questo modo qui. Sai trovare la metrica ![]() che risponde di tale variazione come descritto qui?”.
che risponde di tale variazione come descritto qui?”.
Le equazioni di Einstein descrivono come varia la metrica: se conosci come varia, sai anche trovare la metrica stessa, e se conosci la metrica, conosci il moto di tutti i corpi che sono contenuti nello spaziotempo.
Decodificazione: i due membri
Concentriamoci ora sulla distinzione visiva. Un’equazione serve per trovare qualcosa in funzione di qualcos’altro. Pensa a ![]() , significa: sai trovare quel numero
, significa: sai trovare quel numero ![]() tale che il suo quadrato faccia
tale che il suo quadrato faccia ![]() ?
?
La situazione è molto simile: sai trovare quegli oggetti geometrici dello spazio-tempo ![]() tali che combinati in questo modo si ha uguaglianza con il contenuto di materia ed energia?
tali che combinati in questo modo si ha uguaglianza con il contenuto di materia ed energia?

 , mentre
, mentre 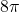 è una semplice costante matematica. D’altra parte
è una semplice costante matematica. D’altra parte  e
e  sono la velocità della luce e la costante di gravitazione universale di Newton, rispettivamente.
sono la velocità della luce e la costante di gravitazione universale di Newton, rispettivamente. La risposta a questa domanda permette di conoscere la curvatura dello spaziotempo in ogni suo punto.
Perché sono chiamate “equazioni” di Einstein, se di equazione se ne vede effettivamente solo una?
In realtà è un modo furbo e sintetico di rappresentarle. L’oggetto ![]() , come visto nell’esempio del lenzuolo, ha in realtà tante componenti. In due dimensioni spaziali (
, come visto nell’esempio del lenzuolo, ha in realtà tante componenti. In due dimensioni spaziali (![]() e
e ![]() ) era un oggetto a quattro componenti. Qui abbiamo
) era un oggetto a quattro componenti. Qui abbiamo ![]() componenti effettive (sarebbero
componenti effettive (sarebbero ![]() , ma alcune sono uguali ad altre, quindi il numero si riduce per simmetria), ad esempio
, ma alcune sono uguali ad altre, quindi il numero si riduce per simmetria), ad esempio ![]() etc.
etc.
Dobbiamo quindi leggere l’equazione di Einstein come ben ![]() uguaglianze indipendenti tra loro!
uguaglianze indipendenti tra loro!
È perfettamente analogo a quel che si fa con i vettori della fisica di Newton: l’equazione ![]() nelle tre dimensioni spaziali sono tre equazioni distinte:
nelle tre dimensioni spaziali sono tre equazioni distinte:
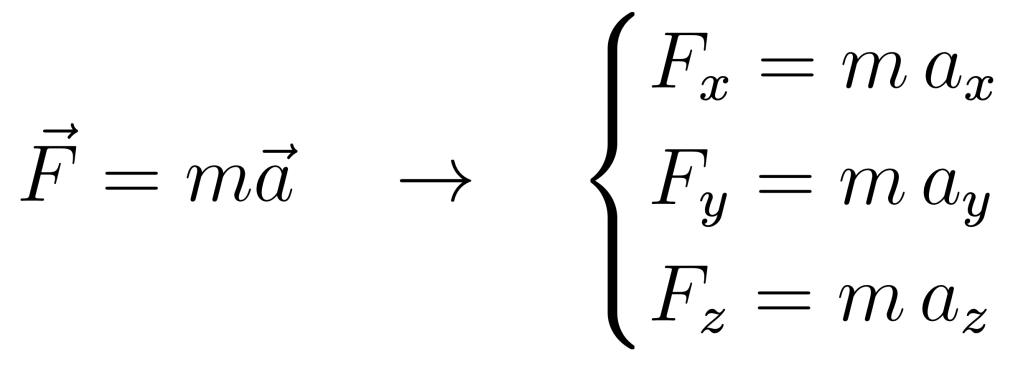
Volendole descrivere con un formalismo più vicino a quello delle equazioni di Einstein, possiamo indicarle con la seguente notazione: ![]() dove
dove ![]() è un indice che scorre sui tre assi cartesiani
è un indice che scorre sui tre assi cartesiani ![]() .
.
Ricordando poi che l’accelerazione è la variazione della velocità nel tempo ![]() , che a sua volta è la variazione della posizione nel tempo
, che a sua volta è la variazione della posizione nel tempo ![]() , potremo indicare con
, potremo indicare con ![]() se
se ![]() è la posizione nell’asse
è la posizione nell’asse ![]() ,
, ![]() o
o ![]() .
.

Le equazioni di Einstein hanno un significato concettuale simile. Nel caso di Newton ci interessa trovare lo spostamento ![]() in funzione del tempo, nota la distribuzione di forze
in funzione del tempo, nota la distribuzione di forze ![]() e la massa del corpo. L’equazione chiave per trovare ciò ci dice “sapendo che lo spostamento varia in questo modo, data la forza, trova lo spostamento ad ogni istante di tempo“.
e la massa del corpo. L’equazione chiave per trovare ciò ci dice “sapendo che lo spostamento varia in questo modo, data la forza, trova lo spostamento ad ogni istante di tempo“.
Nel caso di Einstein le equazioni dicono “sapendo che la metrica varia in questo modo, data la sorgente, trova la metrica in ogni punto dello spazio“. E sono esprimibili in una maniera abbastanza analoga:

In realtà l’informazione contenuta è molto più ricca. Conoscendo ![]() (la materia e l’energia presenti nello spaziotempo) possiamo trovare la forma dello spaziotempo (contenuta in
(la materia e l’energia presenti nello spaziotempo) possiamo trovare la forma dello spaziotempo (contenuta in ![]() ). Tuttavia la conoscenza di questa forma ci dice pure come si muoveranno massa ed energia.
). Tuttavia la conoscenza di questa forma ci dice pure come si muoveranno massa ed energia.
La materia dice allo spaziotempo come curvarsi, e lo spaziotempo dice alla materia come muoversi
J.A. Wheeler
Un esempio molto semplice di sorgente massa-energia si ha nel caso di fluido perfetto in equilibrio termodinamico. Un fluido perfetto è caratterizzato dalla sua densità volumica ![]() e dalla sua pressione
e dalla sua pressione ![]() . Il tensore
. Il tensore ![]() ha la seguente forma:
ha la seguente forma:

Inserendo ![]() nelle equazioni di Einstein è possibile risalire alla struttura dello spaziotempo
nelle equazioni di Einstein è possibile risalire alla struttura dello spaziotempo ![]() , in riposta alla presenza di questo fluido!
, in riposta alla presenza di questo fluido!
Come mai le equazioni hanno questa forma?
Le equazioni di campo di Einstein hanno una forma poco familiare rispetto alle quantità che si maneggiano di solito in fisica classica. Per realizzare matematicamente quello che Einstein voleva esprimere, e cioè che la fisica non deve dipendere dalle coordinate di chi la sta studiando, era fondamentale che le equazioni per lo spaziotempo fossero tensoriali.
La metrica ![]() è un tensore. La sorgente di massa-energia
è un tensore. La sorgente di massa-energia ![]() è un tensore.
è un tensore.
Un tensore è un oggetto matematico che permette di scrivere equazioni che non dipendono dalle coordinate utilizzate, grazie alla sua proprietà di trasformazione sotto cambiamenti di coordinate.
Questa richiesta complica terribilmente le equazioni della teoria, ma le rende infinitamente eleganti, perché assumono carattere di universalità: sono valide per tutti.
Non importa che coordinate utilizzi per studiare la Gravità: sarà sempre una manifestazione della curvatura dello spaziotempo, studiabile nelle coordinate che più ti tornano comode.
Le equazioni di Einstein sono ENORMEMENTE complicate da risolvere, anche nei casi più semplici. Si tratta di equazioni differenziali alle derivate parziali e non lineari, la cui soluzione analitica si conosce solo per un ristrettissimo numero di situazioni altamente semplificate e simmetriche (per tutto il resto, ci sono i computer).
Ad esempio, concentrandoci sullo spaziotempo vuoto attorno a una distribuzione di massa ![]() a simmetria sferica, il lato destro delle equazioni di Einstein è nullo dato che
a simmetria sferica, il lato destro delle equazioni di Einstein è nullo dato che ![]()
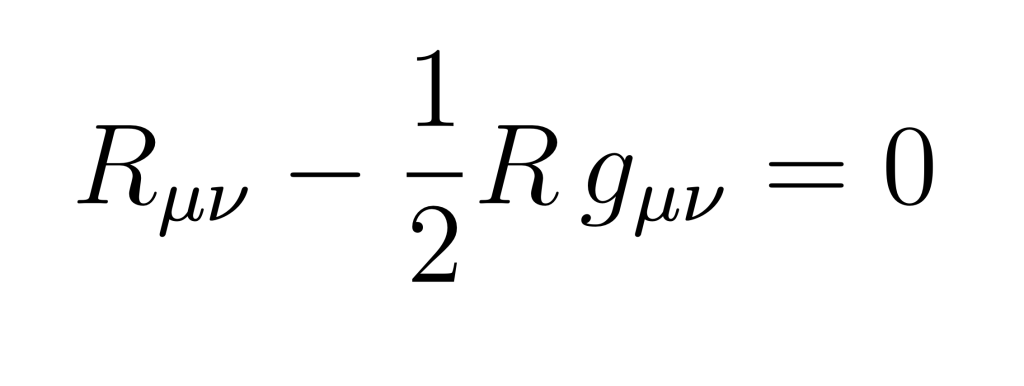
La metrica ![]() che risolve questa equazione (oltre alla soluzione banale di metrica piatta) è data da:
che risolve questa equazione (oltre alla soluzione banale di metrica piatta) è data da:

in cui ![]() è la distanza dalla sorgente di massa
è la distanza dalla sorgente di massa ![]() ,
, ![]() è una coordinata angolare, ed
è una coordinata angolare, ed ![]() è definito come raggio di Schwarzschild
è definito come raggio di Schwarzschild ![]() . Il primo termine in alto a sinistra è
. Il primo termine in alto a sinistra è ![]() , la componente puramente temporale (chiamato anche
, la componente puramente temporale (chiamato anche ![]() ), mentre sulla diagonale abbiamo
), mentre sulla diagonale abbiamo ![]() e
e ![]() , altrimenti indicati con
, altrimenti indicati con ![]() .
.
Per valori della distanza ![]() vicini al raggio di Schwarzschild
vicini al raggio di Schwarzschild ![]() , uno dei termini della metrica (
, uno dei termini della metrica (![]() ) diventa molto grande perché stiamo dividendo per un numero molto vicino a zero. La curvatura dello spaziotempo aumenta sempre di più man mano che la nostra distanza dalla sorgente diminuisce.
) diventa molto grande perché stiamo dividendo per un numero molto vicino a zero. La curvatura dello spaziotempo aumenta sempre di più man mano che la nostra distanza dalla sorgente diminuisce.

Questa metrica ![]() è un esempio di soluzione delle equazioni di Einstein: descrive lo spaziotempo attorno a una massa
è un esempio di soluzione delle equazioni di Einstein: descrive lo spaziotempo attorno a una massa ![]() . Ad esempio lo spaziotempo attorno al Sole ha una struttura di questo tipo. Anche lo spaziotempo attorno alla Terra ha questa struttura. Anche lo spaziotempo attorno a un buco nero.
. Ad esempio lo spaziotempo attorno al Sole ha una struttura di questo tipo. Anche lo spaziotempo attorno alla Terra ha questa struttura. Anche lo spaziotempo attorno a un buco nero.
Dove si nasconde Newton?

La Gravità di Einstein è una versione ultra-sofisticata della Gravità di Newton, in cui i concetti di spazio e tempo si uniscono e diventano dinamici. Nel mondo di Einstein, il tempo è relativo, la velocità della luce è un limite universale, e non esiste l’azione istantanea delle forze, ma tutto deve essere mediato dai campi.
Come faceva Einstein a sapere di aver ragione? Beh, la sua teoria doveva anche essere in grado di riprodurre due secoli di successi della gravitazione di Newton. Scrivendo l’accelerazione come ![]() la legge di Newton per la gravitazione di un corpo attorno a una massa
la legge di Newton per la gravitazione di un corpo attorno a una massa ![]() è
è

L’accelerazione non dipende dalla massa del corpo che cade. Come sai, tutti i corpi accelerano allo stesso ritmo, a parità di distanza dalla sorgente. Questa è una caratteristica unica della Gravità, e ad Einstein venne in mente che proprio per questo motivo la Gravità non è una forza, ma il risultato del moto in uno spaziotempo curvo: tutti i corpi dell’universo si muovono su traiettorie di caduta libera nello spaziotempo, chiamate geodetiche.
Una volta nota la metrica dello spaziotempo, sai come si muoveranno gli oggetti nello spaziotempo.
Nel contesto einsteiniano una geodetica ![]() è una traiettoria nello spaziotempo che soddisfa la seguente equazione:
è una traiettoria nello spaziotempo che soddisfa la seguente equazione:

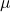 è un indice che scorre tra i valori
è un indice che scorre tra i valori  .
.Espressione che mette un po’ d’ansia se vista per la prima volta, lo ammetto. Sappi solo che serve a trovare una traiettoria nello spaziotempo. Lo spaziotempo è contenuto dentro il simbolo ![]() : la metrica
: la metrica ![]() (e la sua variazione) è proprio contenuta dentro
(e la sua variazione) è proprio contenuta dentro ![]() . Per questo motivo Wheeler diceva che lo spaziotempo dice alla massa come muoversi.
. Per questo motivo Wheeler diceva che lo spaziotempo dice alla massa come muoversi.
La Gravità di Newton si recupera richiedendo che:
- le velocità coinvolte devono essere molto più piccole di quella della luce
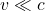 ;
; - la curvatura dello spaziotempo non sia troppo elevata. Ad esempio ci mettiamo a distanza
 , lontani dal raggio di Schwarzschild.
, lontani dal raggio di Schwarzschild.
Così facendo, l’espressione per l’equazione delle geodetiche si approssima così (non è formalmente precisissima, ma mi serve per far rendere l’idea)

Chi è ![]() ? Guardiamo la metrica
? Guardiamo la metrica ![]() trovata sopra:
trovata sopra:

Dunque per trovare l’accelerazione basterà fare la derivata di ![]() rispetto ad
rispetto ad ![]() . Se non sai cosa è una derivata, ti basti sapere che il calcolo produce
. Se non sai cosa è una derivata, ti basti sapere che il calcolo produce ![]() , e che la derivata di una costante fa zero.
, e che la derivata di una costante fa zero.
La velocità della luce ![]() si semplifica in quanto tutta l’equazione delle geodetiche era in realtà moltiplicata da
si semplifica in quanto tutta l’equazione delle geodetiche era in realtà moltiplicata da ![]() (anche se te l’ho nascosto per semplicità). Sostituendo, il risultato è quindi:
(anche se te l’ho nascosto per semplicità). Sostituendo, il risultato è quindi:

e cioè proprio l’espressione newtoniana.
PS. ho scritto un libro di testo che rappresenta proprio ciò che avrei desiderato leggere all’inizio dei miei studi di Fisica teorica, per renderla accessibile agli amatori e insegnare le tecniche matematiche necessarie a una sua comprensione universitaria. Si chiama “L’apprendista teorico” , dai un’occhiata per vedere di cosa si tratta. Il libro è acquistabile su Amazon.




